Sonnenphysik

Die Sonne ist ein aktiver Stern. Dies macht sich unter anderem bemerkbar in Form von Sonnenflecken, Flares, und koronalen Massenauswürfen, deren Häufigkeit dem bekannten 11-jährigen Zyklus folgt. Alle diese Aktivitätsphänomene werden durch das Magnetfeld bestimmt. Die Forschungsabteilung „Sonnenphysik“ des AIP beschäftigt sich mit dem Studium der magnetischen Aktivität in der Sonnenatmosphäre. Da die Sonne unser nächster Stern ist, kann man sie mit ansonsten unerreichbarer räumlicher und zeitlicher Auflösung beobachten. Das AIP führt solche Beobachtungen sowohl mit bodengebundenen Teleskopen im optischen- und im Radiobereich als auch mit Raumsonden durch. Man kann von unserer Sonne lernen, Prozesse auf anderen Sternen zu verstehen („solar-stellare Beziehungen“).
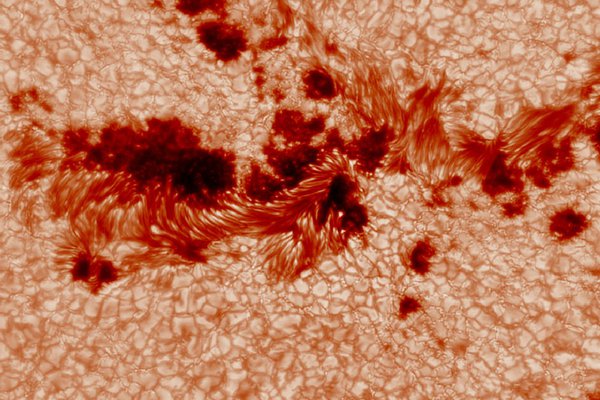
Die Sonne ist der einzige Stern, bei dem sich die Oberfläche bis ins kleinste Detail beobachten lässt. Die optische Sonnenphysik basiert auf Beobachtungen mit hoher räumlicher, zeitlicher und spektraler Auflösung. Mit spektralen Inversionstechniken lassen sich physikalische Zustandsgrößen auf der Sonne bestimmen, zum Beispiel Temperatur, Dichte, Druck, Plasmageschwindigkeiten und das Magnetfeld. Unsere Arbeitsgruppe beschäftigt sich mit der Entwicklung von Instrumenten zur Sonnenbeobachtung, Verfahren zur Bildrekonstruktion, Datenverarbeitung und -analyse sowie spektralen Inversionstechniken – alles mit dem Ziel, so viel Information wie möglich aus dem Licht der Sonne zu gewinnen.
Das AIP ist ein Mitglied des Konsortiums, das die Deutschen Sonnenteleskope am Observatorio del Teide auf Teneriffa betreibt. Unsere Partner sind das Leibniz-Institut für Sonnenphysik (KIS) in Freiburg, das Max-Planck-Institut für Sonnensystemforschung in Göttingen und das Instituto de Astrofísica de Canarias.
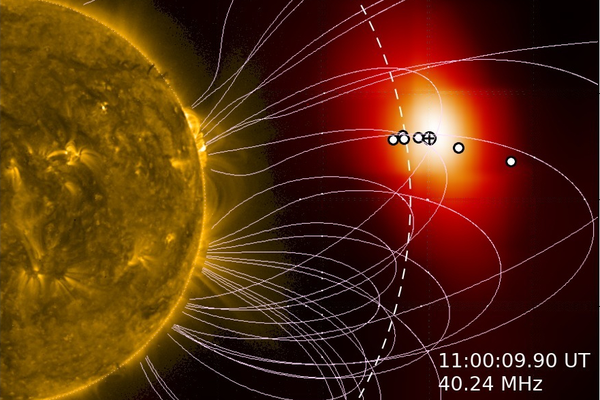
Die Sonnenkorona ist die äußerste Schicht der Sonnenatmosphäre und wird vollständig vom Magnetfeld kontrolliert. Die in koronalen Magnetfeldern gespeicherte Energie kann plötzlich im Rahmen einer Sonneneruption freigesetzt werden. In einem solaren Flare werden dabei Teilchen beschleunigt und Plasma auf hoher Temperaturen geheizt, während bei einem koronalen Massenauswurf magnetisierte Plasmawolken in den interplanetaren Raum hinausgeschleudert werden.
Diese Prozesse können mit Röntgen- und Radiobeobachtungen studiert werden. Daher beteiligt sich das AIP an Weltraummissionen wie Solar Orbiter und betreibt eine LOFAR-Station zur Messung der solaren Radiostrahlung. Wichtige Werkzeuge sind dabei die bildgebende Spektroskopie und die Anwendung der kinetischen Plasmatheorie. Unser Ziel ist hier, die Energiefreisetzung und Teilchenbeschleunigung in der Korona besser zu verstehen.
Die Sonnenaktivität hat auch Einfluss auf unsere technische Zivilisation, insbesondere durch Sonneneruptionen. Dieser Einfluss der Sonne auf unsere Erde wird als „Weltraumwetter“ bezeichnet. Das Studium der Sonnenaktivität ist also nicht nur für die astrophysikalische Grundlagenforschung, sondern für die Gesellschaft schlechthin von Interesse.