Solar Physics

The Sun is an active star. Well-known signatures of the 11-year activity cycle are sunspots, flares, and coronal mass ejections. All activity phenomena are determined by the solar magnetic field. Our work in the research section “Solar Physics” is focused on the observation and analysis of the magnetic activity in the solar atmosphere. Since the Sun is our nearest star, it can be observed with otherwise unattainable spatial and temporal resolution. The AIP performs such observations with ground-based telescopes in the optical and radio range as well as with space probes. Learning from the Sun to understand other stars – this is one aim of the research topic “Solar-Stellar Connection”.
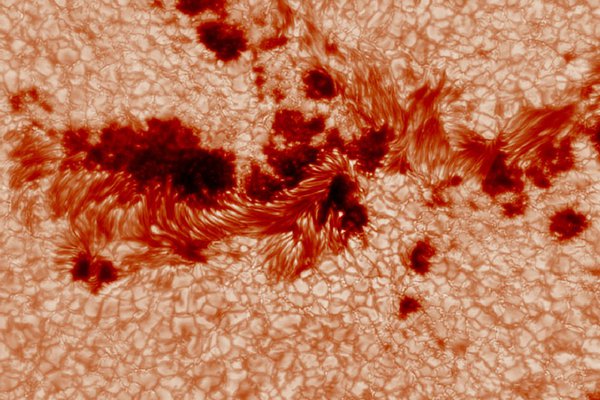
The Sun is the only star where we can observe the intricate detail of stellar surfaces. Optical solar physics focuses on high spatial, temporal, and spectral resolution observations of the solar atmosphere with the aim to derive physical parameters such as temperature, density, plasma velocities, and the strength and direction of the magnetic field. In our research group, we combine expertise in solar instrumentation, image restoration, data analysis, and spectral inversion codes to derive as much information as possible from the Sun's photons.
AIP is a partner of the German solar telescopes operated at the Observatorio del Teide, Tenerife, Spain. Our partner institutes are the Leibniz Institute for Solar Physics (KIS) in Freiburg, the Max Planck Institute for Solar System Research in Göttingen, and the Instituto de Astrofísica de Canarias.
The solar corona is the outermost layer of the solar atmosphere and is completely controlled by the magnetic field. The energy stored in coronal magnetic fields can be suddenly released in a solar eruption. In a solar flare, particles are accelerated and plasma is heated to high temperatures, while in a coronal mass ejection, magnetized plasma clouds are ejected into interplanetary space.
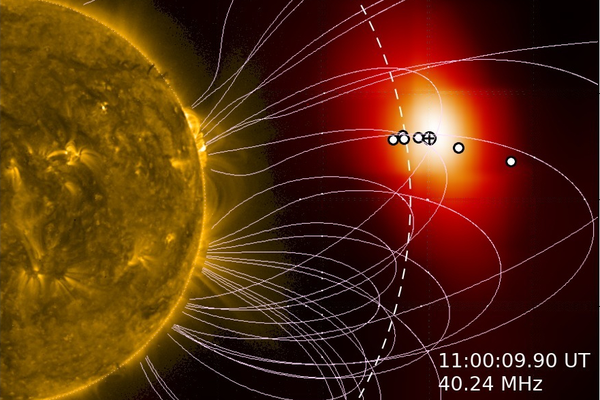
These processes can be studied with X-ray and radio observations. Therefore, AIP participates in space missions such as Solar Orbiter and operates a LOFAR station to measure solar radio emission. Important tools are imaging spectroscopy and the application of kinetic plasma theory. Our goal here is to better understand energy release and particle acceleration in the corona.
Solar activity also influences our technical civilization, in particular due to solar eruptions. The impact of solar activity on the terrestrial surroundings is summarized under the term “Space Weather”. An improved understanding of solar activity is thus not only important for astrophysics, but for human civilization in general.