Scheduling as an optimisation problem
Scheduling tasks on a system with limited resources such as scheduling astronomical observations on a limited set of intruments/telescopes/times has reminiscences to some well-known NP-hard problems. At its core, scheduling is an optimization problem with discrete variables. Starting from a pool of possible observations, the task is to select the observing sequence that maximizes/minimizes the value of some given objective function, which could be as simple as maximize shutter-open time or minimize target airmasses, but usually much more complex objective function will be used.
For any point t in time, an observing block is either executed or not (an observation can not be scheduled partially), thus scheduling differes from more standard optimization problems with continuous variables in the respect that the input variables (task scheduled or not) have only two values, making it a subclass of the so-called integer programming, which is at least NP-complete.
Looking at Karp's classical 21 NP-complete problems, scheduling is similar to the Knapsack problem (how do I optimally fill a knapsack): The knapsack is the allocable time span in question (e.g., a single night) and the items to pack in the knapsack are the observations with individual observing times and individual scientific returns. Classic Knapsack problems have items with constant weights and values, which is not always strictly fulfilled in scheduling observations: the time it takes for an observation (i.e. the weight of the item) may depend on its position in the sky, while the value (i.e. the scientific return) may depend on the exact observing time, but in genereal the reminescence of the the scheduling problem to the Knapsack problem is quite obvious.
Another of Karp's problems is the Job shop problem where the task is to distribute a number of jobs with varying processing time on a set of machines in an order to minimize the makespan, i.e., the total time to complete. The famous traveling salesman problem can be understood as a JSP with a single machine (the salesman), its jobs the different cities to visit. Similarly, on a single telescope, scheduling observations can be seen as a job shop problem with the aim to minimize the totally elapsed observing time. A variant of the job shop problem, the flexible job shop problems, relaxes the requirement that operations that are classically to be executed sequentially on a single machine, may now be scheduled sequentially on a (sub)set of identical machines. This represents scheduling in a network of robotic telescopes.

Example of a one-dimensional (constraint) knapsack problem: which boxes should be chosen to maximize the amount of money while still keeping the overall weight under or equal to 15 kg? A multiple constrained problem could consider both the weight and volume of the boxes. (Solution: if any number of each box is available, then three yellow boxes and three grey boxes; if only the shown boxes are available, then all but not the green box.)
Credit: by Dake, CC BY-SA 2.5, via Wikimedia Commons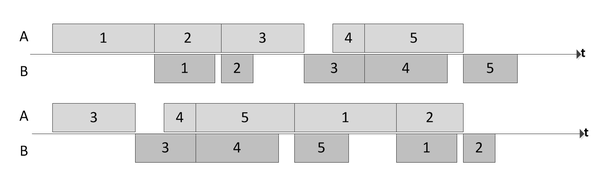
Timelines for a no-wait flow-shop scheduling of five jobs on two machines, A and B. When A finishes a job, B must continue with it immediately. At the top the jobs are processed in the order 1-2-3-4-5 and at the bottom in the order 3-4-5-1-2. The processing times of the jobs on each machine are the same in the two cases, but the bottom case has a smaller total makespan from the start of the first job on machine A to the end of the last job on machine B.
Credit: Klever, CC BY-SA 3.0, via Wikimedia Commons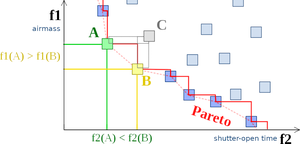
Example of a Pareto frontier. The boxes represent feasible choices. Point A and B represent optimal choices in the Pareto sense, but not C.
Credit: by Johann Dréo (User Nojhan) CC BY-SA 3.0, via Wikimedia CommonsOne fundamental concept in standard optimization is the necessity to define the objective function a priori. For many applications, this is uncritical, but for science-related optimization subsumed with the unspecific term 'scientific return', it may be beneficial if the concrete pick can be adopted during some later decision phase.
A Pareto optimal solution is any feasible solution of a multi-objective optimization problem, that satisfies all constraints of the problem, and, at the same time, cannot be improved further without degrading at least one other objective function. All these possible solutions span the Pareto frontier; once this is defined, different norms applied to the solution vectors a posteriori can then yield a single schedule.
Pure Constraint satisfaction problems are problems with a constant objective function, but with a couple of side constraints that must be satisfied in order to produce a valid solution. A famous example is the eight queens puzzle, where eight quuens have to be placed on a checkboard such that no queens threaten each other. An astronmoical schedule can also be considered to satisfy certain side constaints like target visibility (including moon distance), calibration requirements and required instrument setup, thus long-term planing may be satisfactorally solved if all constraints are considered. Short-term scheduling with non-constant objective functions may then be executed on smaller, e.g., non-violating samples. This approach has been successfully demonstrated on scheduling the Hubble space telescope, where the long-term planning ('cycles') was considered as a plain CSP with a program named SPIKE, short-term scheduling on time-bases of a week were then further optimized with a greedy schema called SPSS (Science Planning and Scheduling System).
How scheduling can be solved
The eight queens example is illustrative to see, how fast NP-complete problems can get computationally cumbersome. Placing 8 queens on 64 tiles yield 64C8 or 4,426,165,368 possible combinations, requiring a single queen at a single row/column, still retains 88 =16,777,216 possible combinations. Using symmetries of the problem, a 8!=40320 possibilities remain. This is easily handable by brute-force techniques, but already at a 20x20 board, one has to consider 20!~2.433 × 1018 possibilities. Similar arguments hold for scheduling observations, thus brute-force attacks are deemed to fail. But there is rescue: If one is interested in not the single one, best solution, including prove that there is no better solution, heuristics come into play. On the following page, a few heurisitc schemes useful in scheduling purposes plus some use-cases are listed.
- Greedy Algorithms like Hill Climbing
- Simulated Annealing
- Simplex Algorithm for linear programming
- Evolutionary Alogrithms/Genetic Algorithm
- Ant Colony/Particle Swarm Optimization
- Neural Networks