Greedy Algorithm
A greedy algorithm in optimiziation problems tries to iteratively improve a solution by maximizing the objective function. Any greedy algorithm starts from a current solution and tries to improve on it by choosing its next candidate solution by selection of a, normally small, step according to some step-selecting function; if the step can be applied at all, the objective function reveals if the solution is improved. If so, the trial solution is accepted as the currently best solution, if not a new step is chosen (i.e. by simply reducing the step width) until an improvment can be achieved or the algorithm has to stop. Normally, a convergence criterion also allows to end the search before too many steps are undertaken that do not substantially improve the objective function further. A straight-forward step-selectiong function can be the local gradient of the objective function.
Greedy algorithms are normally fast, and, if the problem is known to be convex (or precisely, if it can be reduced to a problem with optimal substructures), it will converge to the globally optimal solution, but the thread of being trapped in a local maximum is imminent and can be shown in simple examples:
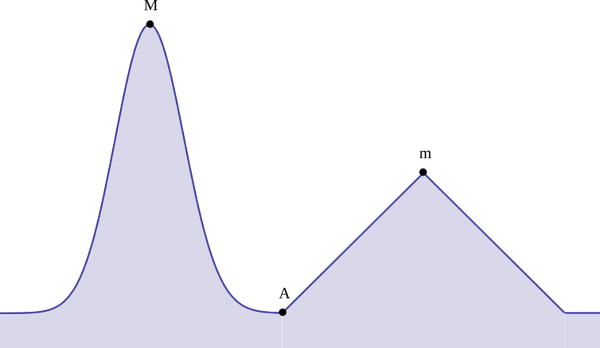
A hill climbing algorithm that will fail to reproduce the correct result, namely summit point M. Instead, it will converge to the local maximum m. A slight start in the starting position, i.e., a tiny shift of A to the left would have produced the correct result.
Credit: Tos (https://commons.wikimedia.org/wiki/File:Greedy Glouton.svg), „Greedy Glouton“, converted to png von TG, https://creativecommons.org/licenses/by-sa/3.0/legalcode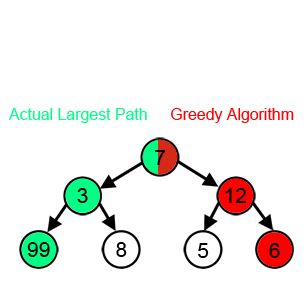
Example of a simple decision tree, where a greedy algorithm will not choose the correct path. The highest gain is the left path (green), but a greedy algorithm will follow the red path.
Credit: Swfung8 (https://commons.wikimedia.org/wiki/File:Greedy-search-path-example.gif), „Greedy-search-path-example“, converted to single png, starting point half coloured von TG, https://creativecommons.org/licenses/by-sa/3.0/legalcodeAs you can see above, even in the one-dimensional case, greedy algortihms can be trapped in a local maximum. Sometimes restarting from different points can improve the situation, like in the hill-climbing scenario. There, if the starting points are sampled dense enough, eventually the algortihm will converge to the global maximum. The situation in a multi-dimensional scenario is normally even worse, with different length-scales in different dimension making alternate sampling cumbersome. Note that convex problems can always be solved with greedy algortihmns.